ChainerRL - Deep Reinforcement Learning Library

By Shohei Hido
Feb 22, 2017
In General

Chainer-based deep reinforcement learning library, ChainerRL has been released. https://github.com/pfnet/chainerrl

(This post is translated from the original post written by Yasuhiro Fujita.)

Algorithms

ChainerRL contains a set of Chainer implementations of deep reinforcement learning (DRL) algorithms. The followings are implemented and accessible under a unified interface.

Deep Q-Network (Mnih et al., 2015)
Double DQN (Hasselt et al., 2016)
Normalized Advantage Function (Gu et al., 2016)
(Persistent) Advantage Learning (Bellemare et al., 2016)
Deep Deterministic Policy Gradient (DDPG) (Lillicrap et al., 2016)
SVG(0) (Heese et al., 2015)
Asynchronous Advantage Actor-Critic (A3C) (Mnih et al., 2016)
Asynchronous N-step Q-learning (Mnih et al., 2016)
Actor-Critic with Experience Replay (Wang et al., 2017)
etc.

Examples

The ChainerRL library comes with many examples such as video gameplay of Atari 2600 using A3C,

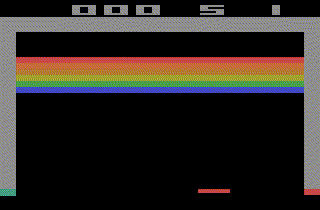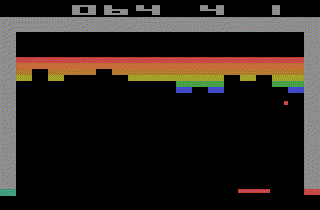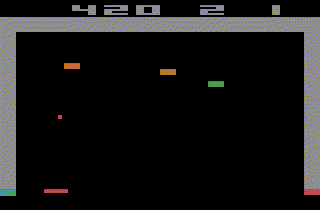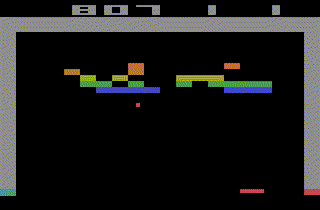
Atari 2600 play

and learning to control humanoid robot using DDPG.

Humanoid

How to use

Here is a brief introduction to ChainerRL.

First, user must provide an appropriate definition of the problem (called “environment”) that is to be solved using reinforcement learning. The format of defining the environment in ChainerRL follows that of OpenAI’s Gym (https://github.com/openai/gym), a benchmark toolkit for reinforcement learning. ChainerRL can be used either with Gym or an original implementation of environment. Basically, the environment should have two methods, reset() and step().

1
2
3
4
5
6
env = YourEnv()
# reset() returns the current observation given the environment
obs = env.reset()
action = 0
# step() sends an action to the environemnt, then returns 4-tuple (next observation, reward, whether it reachs the terminal of episode, and additional information).
obs, r, done, info = env.step(action)

In DRL, neural networks correspond to policy that determines an action given a state, or value functions (V-function or Q-function), that estimate the value of a state or action. The parameters of neural network models are then updated through training. In ChainerRL, policies and value functions are represented as a Link object in Chainer that implements __call__() method.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class CustomDiscreteQFunction(chainer.Chain):
    def __init__(self):
        super().__init__(l1=L.Linear(100, 50)
                         l2=L.Linear(50, 4))
    def __call__(self, x, test=False):
        h = F.relu(self.l1(x))
        h = self.l2(h)
        return chainerrl.action_value.DiscreteActionValue(h)
 
class CustomGaussianPolicy(chainer.Chain):
    def __init__(self):
        super().__init__(l1=L.Linear(100, 50)
                         mean=L.Linear(50, 4),
                         var=L.Linear(50, 4))
    def __call__(self, x, test=False):
        h = F.relu(self.l1(x))
        mean = self.mean(h)
        var = self.var(h)
        return chainerrl.distribution.GaussianDistribution(mean, var)

Then “Agent” can be defined given the model, an optimizer in Chainer, and algorithm-specific parameters. Agents execute the training of the model through interactions with the environment.

1
2
3
4
q_func = CustomDiscreteQFunction()
optimizer = chainer.Adam()
optimizer.setup(q_func)
agent = chainerrl.agents.DQN(q_func, optimizer, ...)  # truncated other parameters

After creating the agent, training can be done either by user’s own training loop,

1
2
3
4
5
6
7
8
9
10
11
12
13
# Training
obs = env.reset()
r = 0
done = False
for _ in range(10000):
    while not done:
        action = agent.act_and_train(obs, r)
        obs, r, done, info = env.step(action)
    agent.stop_episode_and_train(obs, r, done)
    obs = env.reset()
    r = 0
    done = False
agent.save('final_agent')

or a pre-defined training function as follows.

1
2
3
chainerrl.experiments.train_agent_with_evaluation(
    agent, env, steps=100000, eval_frequency=10000, eval_n_runs=10,
    outdir='results')

We also provide a quickstart guide to start playing with ChainerRL.

As ChainerRL is currently a beta version, feedbacks are highly appreciated if you are interested in reinforcement learning. We are planning to keep improving ChainerRL, by making it easier to use and by adding new algorithms.

About Chainer

Chainer is a Python-based, standalone open source framework for deep learning models. Chainer provides a flexible, intuitive, and high performance means of implementing a full range of deep learning models, including state-of-the-art models such as recurrent neural networks and variational autoencoders.

Learn More

Chainer Blog